
So clearly on average is different from saying we get this result every single time. In the example from the previous section, that only would have occurred in one special case if we observed individuals A and D. This doesn't mean for any specific observed sample, our sample mean is equal to the true value. Of course, we should stress the on average. But what this results that the expectation of x bar is equal to Mu, means is that on average, our sample mean is equal to the true population mean, i.e., the very parameter we're trying to estimate. So hence there is variation in this sample means which could be observed. We clearly see that different samples lead to different values of that sample mean. And hence when we calculate a descriptive statistic such as the sample mean as we are considering here. Suppose we took repeated samples of the same size from the same population, then inevitably from one sample to another, we would tend to get different members forming that random sample. So in this word of sampling distributions, we should think of it as follows. Now remember the correct interpretation of an expected value.
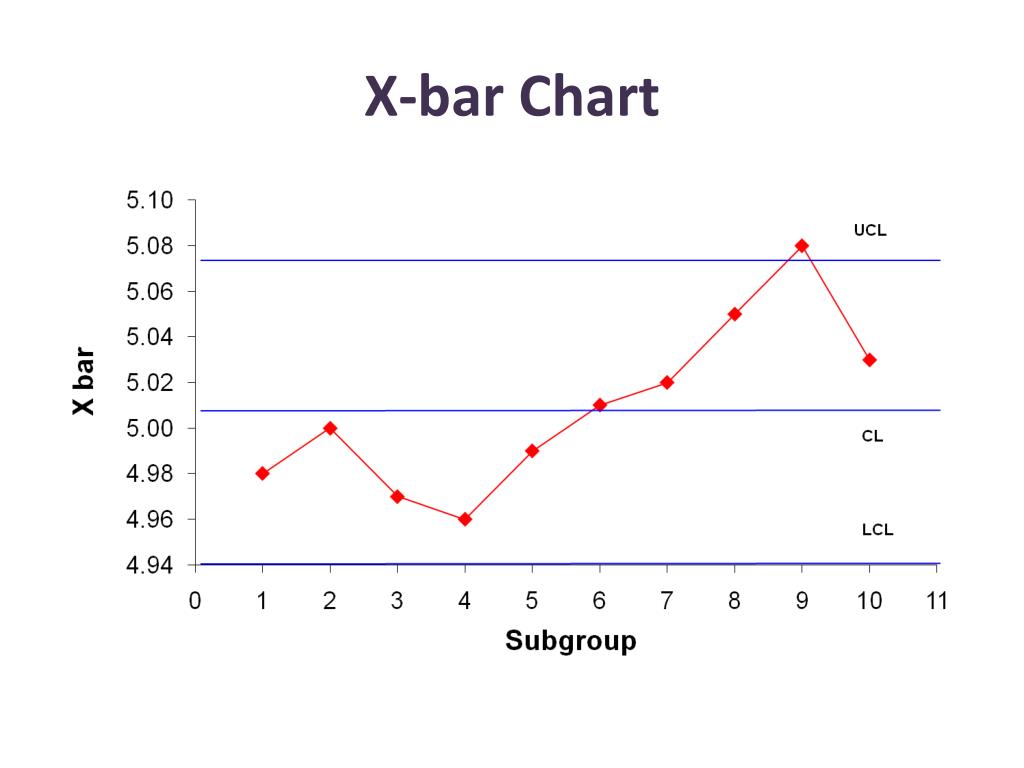
Now this is always going to be the case when we take some simple random sample from some wider population. Which says that the expected value of the sample mean is equal to the true population mean, i.e., the true value of the parameter of interest. Now this is a fascinating and very useful result. Now you may recall 6, in terms of thousands of pounds, represented the population mean. So if we do, for example, 3.5, the smallest observed value of x bar multiplied by its probability of occurence of 1 over 15 and then proceed to do this across the entire distribution, we will find that the expectation of x bar is equal to 6. Taking different values depending on which random sample is observed and we have the probabilities of occurrence for each.
We have a random variable, the sample mean. Well, for our sampling distribution of x bar, we don't deviate from this. i.e., take each value of x, multiply it by its probability of occurence, and then sum these across all values of the variable.

And remember the technique for doing so was to take a probability weighed average. From that point we were then in a position to work out the expectation of that random variable. Where by we derive some simple probability distributions i.e., we have sample space of some random variable x and to each value we attribute it its probability of a current. So relating this back to our work in week 2. Now keep in mind that the sampling distribution is simply a probability distribution of some descriptive statistic. In the previous section, we derived our first sampling distribution of the sample mean x bar. Key topics include quantifying uncertainty with probability, descriptive statistics, point and interval estimation of means and proportions, the basics of hypothesis testing, and a selection of multivariate applications of key terms and concepts seen throughout the course. In this course we consider many useful tools to deal with uncertainty and help us to make informed (and hence better) decisions - essential skills for a lifetime of good decision-making. Whether a good future or a bad future, it would be a known future. While uncertainty makes decision-making difficult, it does at least make life exciting! If the entire future was known in advance, there would never be an element of surprise.
To study, or not to study? To invest, or not to invest? To marry, or not to marry? Indeed, we should be on the look-out for "black swans" - low-probability high-impact events. We live in an uncertain and complex world, yet we continually have to make decisions in the present with uncertain future outcomes.


 0 kommentar(er)
0 kommentar(er)
